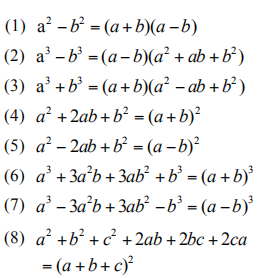SAT数学一直在SAT考试的总分中占据重要的位置，首先我们看一下SAT数学的考试范围分布情况：

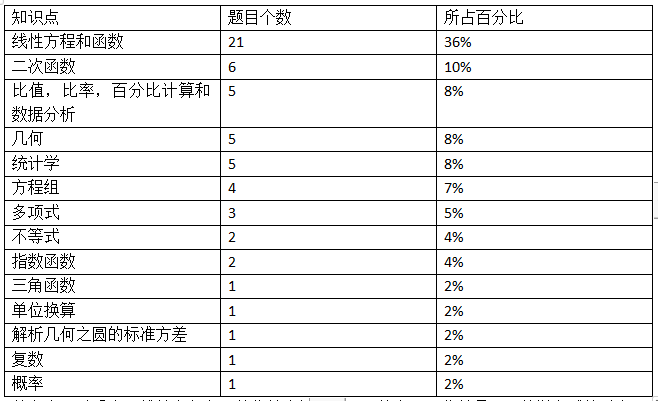
从上表可以看出，线性方程和函数依然占据了近1/3的考题，依然是SAT数学考试的重点。

不同的是，统计学初步知识，比值和百分比计算，数据分析和几何问题有所增加。特比是在统计部分中连续出现关于箱线图，四分位数的考题，这在之前是没有出现过的。

线性方程和函数高频考点

在线性方程和函数中，关于直线的部分是一个非常高频考点，包括斜率，直线的方程，斜率与直线的对应关系，直线的实际应用 （x-intercept和y-intercept）。

1. 首先要知道最基本的斜率的意义以及公式：斜率（slope），表示一条直线相对于横轴的倾斜程度。给定两个点（x1,y1), （x2,y2), 那么通过这两点的直线斜率为k= 。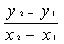

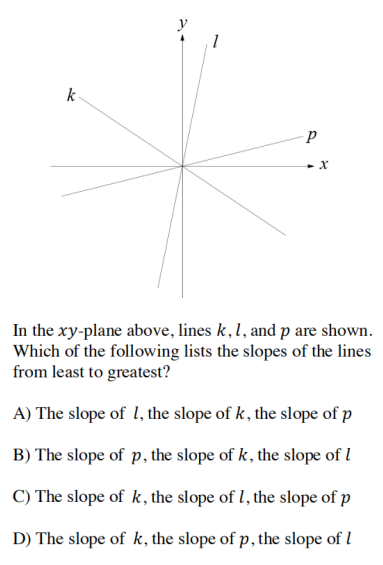
同时， 如果斜率为正，那么这个直线是斜向上（左图）；斜率为负，直线是斜向下的（右图）；平行于X轴，斜率为0；垂直于X轴，斜率undefined。除此之外，还可以通过直线与x轴的夹角进行判断，若为锐角，斜率为正；若为钝角，斜率为负。通过夹角这个方法我们还可以判断斜率的大小，夹角越大，斜率越大 （注意正负号）。

例如2019年5月亚太真题中：通过直线k和x轴夹角为钝角可以知道k的斜率为负，接着直线L和P的夹角可以看出L 的斜率大于P 的斜率，从而得到答案D。

2. 同样在平面坐标系中直线与方程的关系中平行和垂直也是需要我们注意到的高频考点，解题的关键在于抓住两条直线平行时，斜率相同，截距不同，垂直时，斜率互为负倒数。例如2017年11月北美真题section 4的36题

3. 

类似的题目在2018年3月北美section3第4题，section4第24题，2018年5月北美section3第16题，section 4 第35题，2018年5月亚太section 4第19题等

4. 如何在通过题目给出的信息找到相应的直线方程也是一大考点，例如下题（2016年10月北美）可以根据图形知道（2，4）和（0,1）两点求出斜率，继而进行后续的计算。

Line m in the xy-plane contains the point (2,4) and (0,1). Which of the following is an equation of line m?

A) y=2x+3

B) y=2x+4

C) y=3/2x+3

D) y=3/2x+1

类似的题目在2018年3月北美section3第1题，section4第30题，2018年3月亚太section 3第18题，section4第9题，26题，2018年5月北美section3第6题，section4第13题，第25题，2018年5月亚太section3第2题等。

5. 通过直线方程解决实际问题也是我们这一类的高频考点。一般会有两个考点，一，了解截距和斜率在应用题中的实际意义，截距一般指当x=0时，y值的初始意义，斜率一般指当x值增加/减少的时，对y值的变化影响。二，如何根据应用题信息求得直线方程

例如2016年5月北美真题，这类题目的重点在于，根据题意，找到相应的坐标，从而求出斜率，得到直线方程。例如，这题，可以通过图标知道两个坐标（128，950）和（176，1310）从而求出斜率为7.5，直接可以得到答案D，不需要在继续进行复杂的计算。大家做这类题目时，可以采取这种方法，既比较省时，也可以保证正确率。

例如上面2016年5月亚太的题目，问常数12的意义，即y-intercept的意思。一般情况下，y的截距指，当变量为0时，方程的初始意思，按照这个原理去找，会发现B符合我们的答案，在没有买票的情况，所需要给的费用。若问斜率的意义时，一般指变量增加减少对总量的影响。例如下面这题，问的是增加一杯茶对茶包数量的影响，其实找到斜率为1即可。因为斜率为1，茶包数量的变化与茶的变化波动则是1包，答案为B。

类似的题目在2018年3月北美section3第2题，2018年3月亚太section 3第2题，2018年5月北美section3第1题，section4第4题，第25题，2018年5月亚太section4第28题等。

SAT常见数学公式补充

大家在备考的过程中，会有一些基本的公式需要整理，给大家整理出一些常用的公式：

1. 

2.指数运算法则为

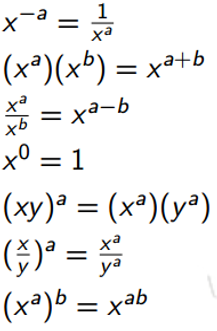
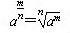
3.圆的标准方程(x-a)²+(y-b)²=r²中，有三个参数a、b、r，即圆心坐标为(a，b)和半径r

4. 常见的完全平方公式